半導体2次元電子系と量子ホール効果(対象:高校生〜大学院生)
半導体とは?
1.半導体とは金属(電気を流す)と絶縁体(電気を流さない)の中間の性質を持つ物質である。(?)
2.半導体においては、電子が詰まっている価電子帯と空の伝導帯との間のエネルギーギャップが小さいため、室温程度の温度でも価電子帯から伝導帯に熱励起することができ、伝導帯の電子と価電子帯にできた正電荷をもつ穴(正孔)が電気を運ぶ。(?)
このような説明を良く見かけますが、誤解を招く可能性があるので補足しておきます。例えば、最も代表的な半導体であるシリコン(Si)の純粋な結晶を考えると、価電子帯から伝導帯への熱励起によってできるキャリア(電気の運び役)の数は、1立方cmあたり1010個程度です。地球上の人口程度ですので、一見多く感じるかもしれませんが、原子の数と比べると非常に少なく、室温における純粋なSiはほとんど絶縁体といってもよい状態にあります。
実は、デバイスとして使われているSiの電気的性質を決めているのは、わざと添加した不純物です。IV族のSiの結晶中にV族のP(リン)を入れてやると、Pは電子を一個多く持っていますので、伝導帯に電子を供給することができます。このとき、Pはドナーと呼ばれます。また、III族のB(ボロン)を入れると、Bは電子が一個だけ不足していますので、価電子帯に正孔ができます。このとき、Bはアクセプターと呼ばれます。伝導帯に加えられた電子が活躍する半導体をn型半導体、価電子帯の正孔が活躍する半導体をp型半導体と呼びます。nとpはそれぞれnegativeとpositiveに対応し、キャリアの電荷の符号を意味します。不純物添加を制御して、一つの半導体結晶の中にn型の領域とp型の領域を共存させてやるとダイオードができます。pからnに電流を流す場合、境界に正孔と電子が次々とやってきてと結合します。このときのエネルギーが光となって放出されるものが発光ダイオード(LED)です。逆に、nからpに電流を流そうとした場合、境界付近のキャリアがいなくなってしまい、電流がすぐに流れなくなります。電流の向きによって流れやすさが変わるダイオードの性質は、さまざまなところで役に立っています。
また、不純物を添加しない場合でも、半導体表面の上に絶縁膜を作り、さらにその上に金属膜(ゲート)を作製して、金属と半導体との間に電圧(ゲート電圧)をかけると酸化膜との界面近くにキャリアを作り出すことができます(下図も参照)。ゲート電圧の符号は作りたいキャリアの種類に依ります。このようにゲート電圧によって半導体側の電気の流れやすさが変わることを利用した素子を電界効果型トランジスター(field-effect-transistor,
FET)と呼びます。特に、絶縁膜に母体の半導体の酸化膜を利用したものをMOS(metal-oxide-semiconductor)FETと呼びます。
現代文明を支えている半導体を理解する上では、「半導体とは、人間が制御して金属にしたり、絶縁体にすることができる物質である。」と理解した方が良いかもしれません。一方、こうした半導体の性質を利用して、基礎物理の研究の素晴らしい舞台が作られています。整数量子ホール効果、分数量子ホール効果などの大発見がなされた2次元電子系や量子ドット、量子細線などのメゾスコピック系の研究が盛んに行われています。
2次元の国の電子!!
電子を平面に閉じ込めると2次元電子系ができます。そのためには、半導体と別の物質(絶縁体や他の半導体)との界面や表面を利用します。まず、代表的なIII-V族化合物半導体であるGaAsとGaの一部をAlに変えたAlxGa1-xAs(xは0.2-0.3程度)とのヘテロ界面(下、左図)を考えましょう。
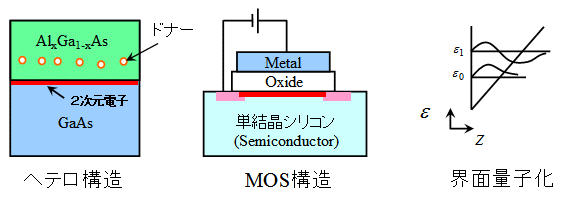
このような構造は分子線エピタキシー法による結晶成長などによって作製されます。GaAsの伝導帯の底のエネルギーがAlGaAsよりも低いために(電子親和力が高い)ために、AlGaAs側に入れたドナー(Siなど)から供給された電子は、GaAs側に落っこちます。GaAs中の電子は、正イオンとなったドナーからの引力によってAlGaAsとの界面に束縛された状態になります。しかし、界面に沿った方向には自由に動けます。通常、イオン化したドナーは電子の運動にとって主要な散乱体となるのですが、ヘテロ構造の場合、ドナーと電子が離れた場所にありますので、非常に散乱の少ない2次元電子系が得られます。
上述のSi-MOSFETにおいても、2次元電子系が作られます。この場合、Si中の電子は金属ゲートからの電場によって界面に束縛された状態になります。
接合面における障壁と電場とで作られる三角ポテンシャルに閉じ込められた、電子の界面に垂直方向の運動は、量子効果によってとびとびのエネルギー状態を作ります。基底エネルギーと第一励起エネルギーとの間隔が温度よりも十分に大きく、電子の数がそれほど多くないときには、すべての電子が基底状態に収容されるため、界面に垂直な運動に関する自由度はなくなり、私たちは理想的な2次元電子系を手にすることになります。
例えば、半導体(GaAsなど)の薄い層を別の半導体(AlGaAsなど)で上下から挟んでやると(ダブルへテロ構造)、井戸型ポテンシャルを作ることもできます。この場合も、三角ポテンシャルの場合と同様に、2次元電子系が作られます。
これまで研究は、デバイスに閉じ込められた界面の2次元電子に対するものがほとんどでしたが、近年、我々は、超高真空中で結晶を劈開して得られた清浄表面に2次元電子系を作製し、量子ホール効果などの電気伝導現象を観測することに成功しています。
2次元電子と磁場
2次元系がどうやって作られたかについて、ここからは忘れてかまいません。
2次元平面に垂直に磁場をかけてみましょう。平面に沿って動く電子はローレンツ力を感じますが、その結果、サイクロトロン運動と呼ばれる円運動を行います。振動数はωc= eB/m*で与えられます(eは素電荷、m*は電子の有効質量)。
この運動は量子化されて、ランダウ準位と呼ばれる離散的なエネルギースペクトルが形成されることになります。
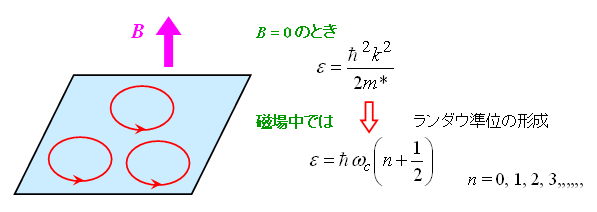
また、電子はスピンs=1/2をもっていますので、各ランダウ準位はゼーマンエネルギーの異なる2つのサブレベルに分裂します。ゼーマン分裂とランダウ準位間隔との比を変えたい場合には、磁場の角度を制御します。
2次元電子系の抵抗測定
2次元電子系の電気伝導の測定にはホールバーと呼ばれる形に加工した試料を使います。
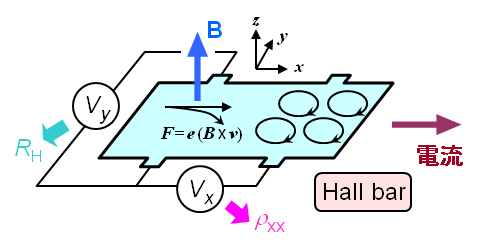
電流方向に生じる電位差から対角抵抗率ρxxが得られます。また、ホール効果による電流に直交した方向の電位差から、ホール抵抗RH(2次元系の場合はρxyに等しい)が得られます。
ランダウ準位充填率とShubnikov-de Haas振動
一本のランダウ準位の単位面積あたりの状態数(電子を収容できる座席の数)は、eB/hで与えられます(hはプランク定数)。(ランダウ準位間隔は磁場に比例しますので、平均的な状態密度は磁場に依らないことになります。)電子密度NsとeB/hとの比ν=Ns/(eB/h)をランダウ準位充填率と呼びますが、磁場が高くなるにつれてν(ニュー)が連続的に小さくなっていきます。νが整数のとき、フェルミエネルギーはランダウギャップの間にありますが、このときに対角抵抗率(青)は極小値をとります。こうして抵抗の磁気振動(Shubnikov-de
Haas振動)が観測されます。
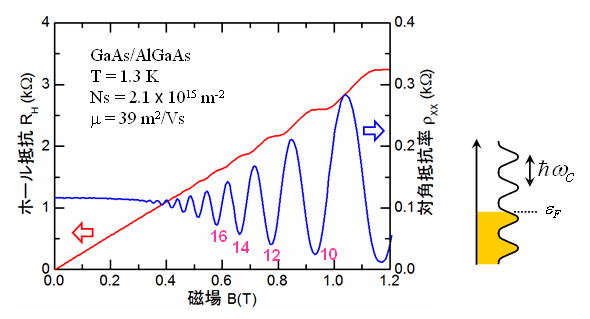
図で極小点に対応したνの値をピンクで示しています。低磁場ではスピン分裂が小さいためにνが偶数の場合にのみ対角抵抗の極小が観測されています。
整数量子ホール効果
高磁場・極低温では、対角抵抗はν=整数において完全にゼロになります。フェルミエネルギーがランダウギャップの間にあるために散逸が起こらなくなったためだと理解できます。電流と電場が直交しているためにジュール発熱はゼロです。このとき、ホール抵抗はh/e2を整数で割った値に量子化されます。これが整数量子ホール効果です(1985年のノーベル物理学賞)。(1)ローレンツ力とホール電場FHの釣り合いの式から電流を運ぶ電子の平均速度がu=FH/Bで与えられる。(2)電子の密度Nsは(eB/h)の整数倍である。(3)電流密度はj=eNsuである。(4)電流もホール電圧もともにチャネル幅に比例するためRH=FH/jである。以上から、少なくともν=整数においてRHが量子化値を取ることがわかります。
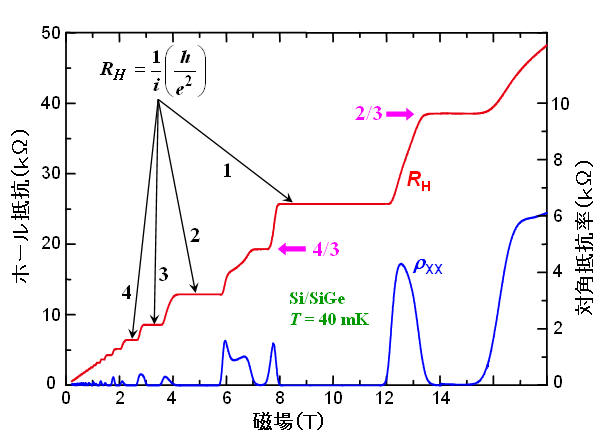
実際には、ν=整数から多少ずれてもRHは量子化され、対角抵抗はゼロのままです。これには不規則ポテンシャルに束縛された局在準位が関連するのですが、ここでは深入りしないことにします。このプラトーの存在により、量子化されたホール抵抗を高精度で測定することができます。量子化ホール抵抗の値が物質の種類に依存しないことは、10-9以下の精度で確かめられており、量子化ホール抵抗は抵抗標準として採用されています。一方で、量子ホール状態における電気伝導の研究は、エッジ状態やブレークダウンなどの興味深い問題とも関連し、非常に奥が深く、活発に研究が行われています。
量子ホール効果を詳しく知りたい人には、たくさんの教科書がありますので、そちらで勉強してください。
また、学部3年生くらいからを対象に簡単な解説を用意しました。(pdfファイル)
分数量子ホール効果
量子化ホール抵抗をRH=h/νe2とおいたとき、νが分数値をとる現象が、分数量子ホール効果(1998年のノーベル物理学賞)です。上図の測定でも4/3や2/3の分数量子ホール状態が観測されています(磁場をさらに強くすると2/5や1/3も見られるはずです)。ν<1ではすべての電子は、最低ランダウ準位に収容されているはずなので、電子状態は電子間のクーロン相互作用によって決まります。完全な多体問題であり、理論家がしのぎを削るテーマです。
参考書:
吉岡大二郎「量子ホール効果」(岩波書店)
中島龍也、青木秀夫「分数量子ホール効果」(東大出版)
など




